在二分类问题中,输出$y\in \{0, 1\}$。同样的,我们也可以用线性拟合来尝试解决二分类问题(如下图左),但数据点比较异常时,容易出现下图右这样的情况:
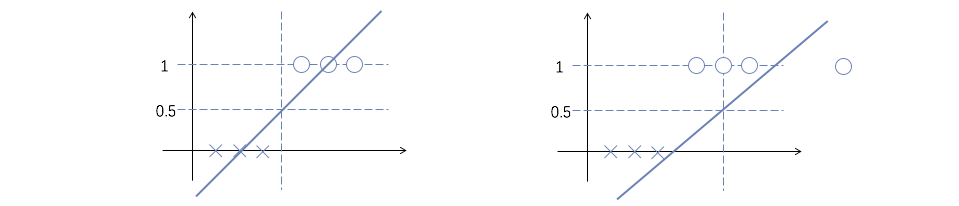
一般,在二分类问题中,我们会选用『logistic函数』来拟合(因为形状像S,又称为『sigmoid函数』):
logistic函数$g(z)=1/(1+e^{-z})$的形状如下: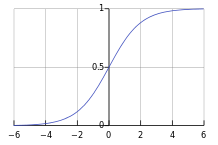
可以定义
于是:
进行极大似然估计:
为了计算方便,定义
利用梯度上升进行求解:
其中
最终的梯度上升结果几乎与线性拟合中的梯度下降结果一样。
在二分类问题中,输出$y\in \{0, 1\}$。同样的,我们也可以用线性拟合来尝试解决二分类问题(如下图左),但数据点比较异常时,容易出现下图右这样的情况:

一般,在二分类问题中,我们会选用『logistic函数』来拟合(因为形状像S,又称为『sigmoid函数』):
logistic函数$g(z)=1/(1+e^{-z})$的形状如下:
可以定义
于是:
进行极大似然估计:
为了计算方便,定义
利用梯度上升进行求解:
其中
最终的梯度上升结果几乎与线性拟合中的梯度下降结果一样。